Implementing Selection Sort in Java
12/11/2020#java #tutorial #algorithms #programming
Selection Sort is a simple sorting algorithm. In this article we are gonna implement it using java to sort an array from smallest to largest element. We are gonna talk about it's time complexity too. Let's dive into it!
Let's start by creating our first java file SelectionSort.java
In this file we are going to create a method called sort that returns an array of ints.
1int[] sort(int[] arr) { 2 int index; 3 //looping the unsorted list 4 for (int first = 0; first < arr.length; first++) { 5 6 } 7}
Here we start by creating a integer variable called index (that we are going to use later) and a loop that iterates through all the array. Then we are going to make index have the same value as first, make another loop and implement our condition... Yeah that's a lot! Allow me to explain.
1int[] sort(int[] arr) { 2 int index; 3 //looping the unsorted list 4 for (int first = 0; first < arr.length; first++) { 5 6 //index starts at first but changes in every loop 7 index = first; 8 9 //then every loop the index is compared with all numbers 10 //except the one we are comparing to (the index) 11 for (int i = first + 1; i < arr.length; i++) { 12 //check if value is lower 13 if (arr[i] < arr[index]) { 14 //if it is, change index to it 15 index = i; 16 } 17 } 18 } 19}
Let's start explaining this second loop we made. This loop is inside the first loop, so every time we iterate the first loop once, we get a value of the list and go through all the elements in the array using the second loop, so we can compare the value we got in the first loop with all the elements in the array with the second loop.
IMPORTANT: In the second loop we make int i = first + 1 because we are looping every item in the list EXCLUDING only the one we are actually comparing, because the value we have is never gonna be smaller than itself.
After the two loops were made we make a condition inside the second loop, where we check if the the items in the for loop (arr[i]) is smaller than the value we got with the first loop (arr[index]) . If the condition is true we make the index, that holds our smaller number so far, be the index of the smaller number found. The if condition checks every number in the second loop until the end, getting the smaller number in the array and saving its index with the index = i .
Now that our second loop got to the end and we have the index of our smallest number we need to swap the position he is in
1int[] sort(int[] arr) { 2 int index; 3 //looping the unsorted list 4 for (int first = 0; first < arr.length; first++) { 5 6 //index starts at first but changes in every loop 7 index = first; 8 9 10 //then every loop the index is compared with all numbers 11 //except the one we are comparing to (the index) 12 for (int i = first + 1; i < arr.length; i++) { 13 //check if value is lower 14 if (arr[i] < arr[index]) { 15 //if it is, change index to it 16 index = i; 17 } 18 } 19 20 //holds the value of the minimum we found 21 int temp = arr[index]; 22 //places the value that was in the start at the place we found our index 23 arr[index] = arr[first]; 24 //puts the value from the index in the start 25 arr[first] = temp; 26 } 27 //terminate the loop and return array sorted 28 return arr; 29 30}
Here I we have all the sort method ready, I put it all completed here so you don't get confused on where the pieces of code are in the big picture, but we are going to be talking about the end, the swap and return part:
1 //holds the value of the minimum we found 2 int temp = arr[index]; 3 //places the value that was in the start at the place we found our index 4 arr[index] = arr[first]; 5 //puts the value from the index in the start 6 arr[first] = temp; 7 } 8 //terminate the loop and return array sorted 9 return arr; 10 11}
I'm gonna talk about this giving an example that was made in CS50 algorithms part (highly recommend), you have two cups, one with a blue liquid and the other with a red liquid. You want to swap the blue liquid of the 1 cup to be in the 2 cup and the red liquid of the 2 cup to be in the 1 cup without mixing. What do you do? A good way to do this is have a "Temporary cup", a 3 cup that will hold your blue liquid, so you can put the red liquid in the 1 cup, and then put the blue liquid in the 2 cup.
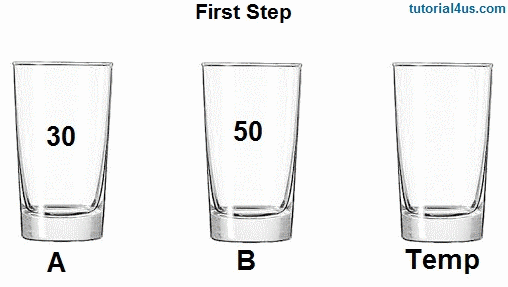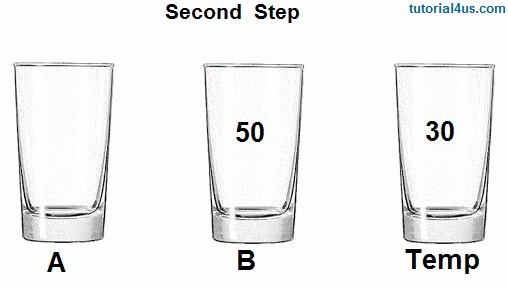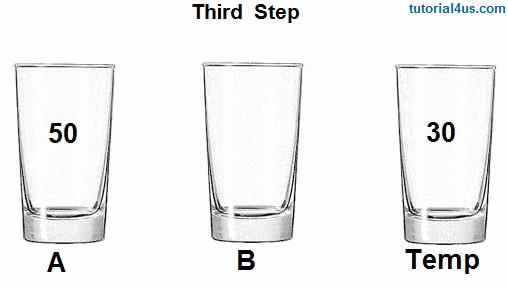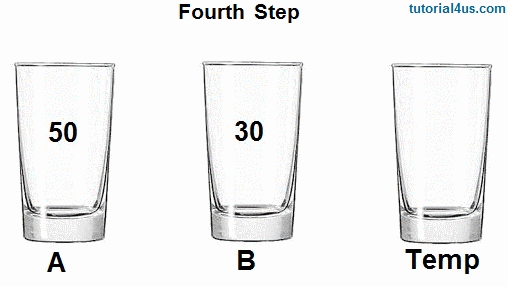
In code we are doing the same thing! We are making a temporary variable int temp and assigning the value of the smallest number we found to it. Then we make the value of arr[index], that is current the smallest number, be the value of the first loop, and we make the value of the first loop be the temporary variable, the smallest number.
With that we made our swap! So after that the first iteration of the first loop finally ends and repeats itself again until we looked at every number and compared, choose and swap then. Now we just need to return the sorted array with return arr .
Time complexity
Before we print make our print method and then execute our code to see everything working let's explain the time complexity of this algorithm. We start the algorithm making a loop that goes through every number in the array. which means that we have a O(n) because n is the number of steps and is = to the number of elements we have in the array. After that we have a second loop, inside the first loop, that iterate through every number in the array too, so that's another O(n). So we have a O(n) that for every n inside of it there's another O(n), that makes O(n X n) or O(n^2). So the time complexity of this algorithm is O(n^2) !
Wait a second...
Maybe you are questioning yourself "But every time we make our second loop we make it be the position of the first loop + 1, so we don't check n entirely in the second loop, so it would be n-1,n-2..." and yes, you are actually right! at the end of the second loop we would be checking just one element, so the time complexity should be something like O(n X 1/2 X n). This is correct, but in the Big O notation we ignore constants like 1/2, so in the end we just have O(n X n) and that's why it stays like that!
Okay that was a mouthful, but we are almost at the end! now we are just going to create the last method, printArray:
1 void printArray(int[] arr) { 2 for (int i = 0; i < arr.length; i++) { 3 System.out.print(arr[i] + " | "); 4 } 5 }
Here we don't need to return anything, we are just making a for loop that goes through all the array and prints the values with a pipe | separating them.
Now we are gonna create a java file to execute and test this algorithm! Let's create a file called SelectionSortMain.java
1package selectionSort; 2 3public class SelectionSortMain { 4 public static void main(String args[]) { 5 SelectionSort selection = new SelectionSort(); 6 7 //create the array 8 int[] arr = {10, 6, 4, 8, 2}; 9 10 //This is gonna print the original array 11 System.out.println("Unsorted array: "); 12 selection.printArray(arr); 13 14 //sort the array 15 selection.sort(arr); 16 17 //used println here just to make a space since we used print in the printArray 18 System.out.println(); 19 20 //print sorted array 21 System.out.println("Sorted array: "); 22 selection.printArray(arr); 23 } 24 25} 26
Here we just create an array, print it unsorted (with our printArray method) and then we use our sort method and print it again, so our output should be this:
1Unsorted array: 210 | 6 | 4 | 8 | 2 | 3Sorted array: 42 | 4 | 6 | 8 | 10 |
And that's pretty much it! Hope this article helped you in some what way. You can check out the repo I made in Github with all the code and with more implementations of DS&A. I'm new to making articles and writing in general but I'm trying to improve! Any questions or suggestions are pretty much appreciated. Good luck on your learning journey!